Limit of a function: how to determine it?

All scientific disciplines are based on mathematics, and data science is no exception. When the problems to be solved are optimization problems, you need to know what the limit of a function is. In this article, you’ll discover how to determine the limit of a function.

Limit: Definition

The limit of a function [latex]f[/latex] is the value the function approaches when its argument approaches a certain value.Mathematically, we write [latex]lim limits_{x to a} f(x) = l[/latex]
We say that [latex]f[/latex] tends towards [latex]l[/latex] when [latex]x[/latex] tends towards [latex]a[/latex].Depending on the case, [latex]a[/latex] and [latex]l[/latex] may be real numbers, or equal to [latex]pm infty[/latex].

Limits of standard functions

– Real-valued finite limits

For example, for [latex]f(x) = x^2[/latex], the limit when [latex]x[/latex] tends towards [latex]2[/latex] is [latex]2^2 = 4[/latex].

– Infinite limits

When the function is well defined at a real number [latex]a[/latex] (it is said to be continuous at [latex]a[/latex]), then the limit at [latex]a[/latex] is exactly [latex]f(a)[/latex].
When the variable [latex]x[/latex] takes on very large values (positively or negatively), we say that [latex]x[/latex] tends towards more or less infinity. In this case, we distinguish between cases where [latex]f(x)[/latex] approaches a finite value and those where [latex]f(x)[/latex] moves away towards infinity. In the former case, [latex]f[/latex] is said to converge, and in the latter, [latex]f[/latex] to diverge.
Below is a table summarizing the limits of common functions at infinity.

When a function admits a finite limit [latex]l in mathbb{R}[/latex] when [latex]x to infty[/latex], then we say that [latex]f[/latex] admits a hor– Infinite limits at a finite value

[latex]
begin{array}{|c|c|}
hline text{Function} & text{Limit} 0, : x to 0 \
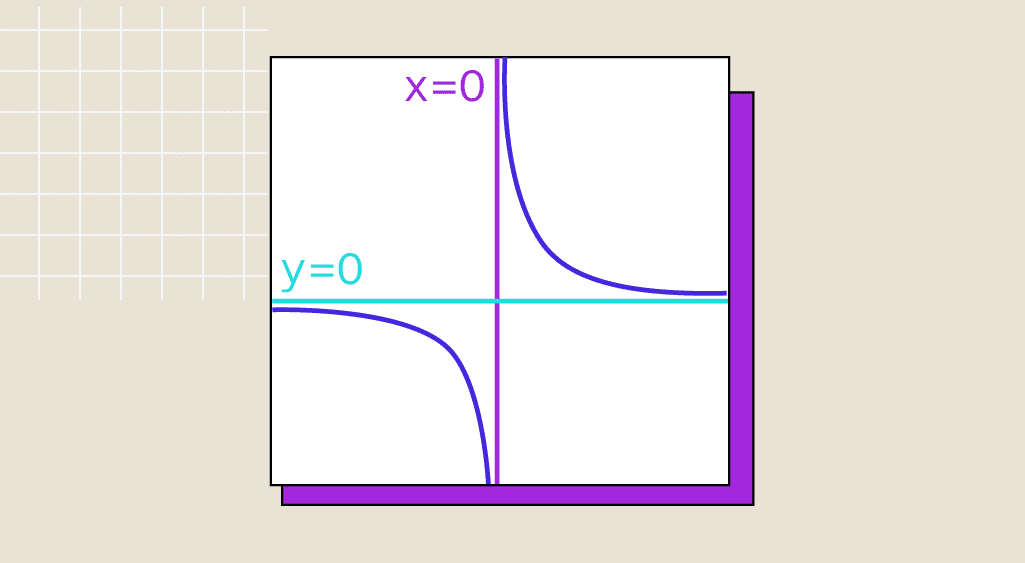
hline f(x) = frac{1}{x} & begin{cases} & +infty text{ si } x gt 0 \ & infty text{ si } x lt 0 end{cases} \
hline nan & nan \
hline f(x) = ln(x) & -infty \
hline f(x) = sqrt{x} & 0 \
hline
end{array}
[/latex]When [latex]lim_{x to a} f(x) = pm infty[/latex], with [latex]a[/latex] a real number, then the curve of [latex]f[/latex] is said to have a vertical asymptote at [latex]a[/latex]. In other words, the curve moves closer and closer to the straight line with equation [latex]x=a[/latex].

Find out more about our Data Science training courses

Limit operations

In most cases, it is possible to perform limit operations to determine the limit.Limit of a sum of two functions


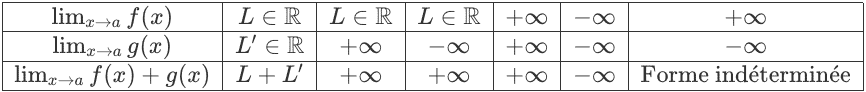
Limit of a product of two functions


Limit of a quotient of two functions


Click on the tables to display them full-screen.

Determining a limit in practice

To determine limits, it’s sometimes simpler to use other functions.
Comparing functions allows you to compare their limits, when they exist.
There are two main properties for comparing functions

– Comparison theorem

Let [latex]f[/latex] and [latex]g[/latex] be two functions defined on an interval [latex]I = [a, +infty[[/latex].
Assume that for any [latex]x in I ; f(x) geq g(x)[/latex]If [latex]lim_{x to +infty}g(x) = +infty[/latex], so [latex]lim_{x to +infty}f(x) = +infty[/latex]
If [latex]lim_{x to +infty}f(x) = -infty[/latex], so [latex]lim_{x to +infty}g(x) = -infty[/latex]

– Gendarme theorem

Let [latex]f[/latex], [latex]g[/latex] and [latex]h[/latex] be three functions Assume that for any [latex]x in I ; g(x) leq f(x) leq h(x)[/latex]If [latex]g[/latex] and [latex]h[/latex] tend to the same limit [latex]l[/latex] in [latex]+infty[/latex], then [latex]lim_{x to +infty}g(x) = +infty[/latex]You now know what a limit is and how to calculate it. Calculating limits allows you, for example, to define the derivative of a function as the limit of a rate of increase. If you’d like to discover all the mathematical concepts involved in data science, we invite you to take a look at our curricula.

Training in Data Science